
En el mundo que nos rodea persisten desde el inicio de los tiempos algunos fenómenos que se escapan del deseable pleno control del ser humano.
La propagación de un incendio, la trayectoria que seguirá el agua en una inundación (o más domésticamente, dónde se habrá generado la filtración que ha provocado una gotera en el techo), las turbulencias aéreas o marinas que provocan incomodidades y a veces desastres, o algo tan banal como conocer si lloverá o hará un calor insoportable el próximo fin de semana. Todos ellos fenómenos de distinta índole y naturaleza, aparentemente.

Si indagamos un poco en lo que los provoca, encontraremos que tienen algo en común: están originados por fluidos. Los fluidos desde un punto de vista físico-químico son conjuntos de partículas unidas entre sí por fuerzas débiles que permiten que ante una fuerza externa las posiciones de sus moléculas varíen, fluyan (de ahí su nombre). Es el caso de los líquidos, los gases y el plasma.
Líquidos y gases se adaptan al lugar en el que se encuentran, pero mientras los primeros son incompresibles (por mucho que los “achuchemos”, su volumen sigue siendo el mismo), los segundos no, aunque si se les deja, tienden a ocupar el mayor espacio posible, se expanden. Los líquidos, además, ejercen presión sobre los cuerpos que se sumergen en ellos y sobre las paredes del recipiente que los contiene (presión hidrostática). La parte de la Física que estudia los fluidos y sus aplicaciones se llama mecánica de fluidos, que se divide en hidrostática (se ocupa de los fluidos en reposo o en equilibrio) y la hidrodinámica (fluidos en movimiento). Llegados a este punto, el lector se estará preguntando: ¿Y qué pintan las matemáticas en asuntos de naturaleza tan física? ¿Me he confundido de sección o se han confundido ellos? Un poco de paciencia, que vamos acercándonos.
En 1822, el matemático e ingeniero francés Claude-Louis Navier (con una extensa carrera investigadora a pesar de fallecer a los 41 años) deduce un sistema de ecuaciones que describe el comportamiento de algunos fluidos. Veinte años después, Sir George Gabriel Stokes, partiendo de un modelo diferente, completa la descripción de esas ecuaciones, bautizadas como ecuaciones de Navier-Stokes en honor a ambos. Simplificando, digamos que se obtienen aplicando los principios de conservación de la mecánica y la termodinámica a un volumen fluido. Así se obtiene la llamada formulación integral de las ecuaciones, aunque se suele trabajar con ellas a partir de su formulación diferencial, como la que aparece en la imagen adjunta (que representa el caso concreto de un fluido viscoso pero incompresible).
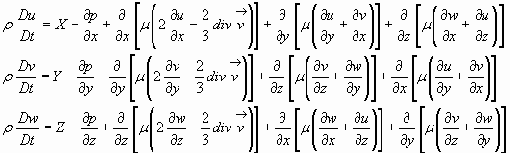
Estas ecuaciones determinan el comportamiento de los llamados fluidos newtonianos. Un fluido newtoniano es aquel cuya resistencia a deformaciones (viscosidad) puede considerarse constante en el tiempo. El ejemplo más socorrido es el agua (viscosidad nula), aunque otros fluidos habituales en nuestro quehacer diario, bajo condiciones normales de presión y temperatura, se comportan como newtonianos, como el aire, algunos aceites, etc. Fluidos no newtonianos serían los geles, el pegamento, la miel o la sangre, por citar algunos de los más comunes. Para los fluidos newtonianos, si representáramos gráficamente la relación entre la fuerza ejercida (en un eje de coordenadas) y la velocidad de deformación del fluido (en el otro eje) nos aparece una línea recta (dicho de otro modo, esa relación es lineal), por lo que se trata de los fluidos más sencillos de describir.
Tratemos al menos de saber qué representa cada término de las ecuaciones: hay valores constantes (ρ la densidad, μ la viscosidad), las velocidades de desplazamiento en cada dirección (vx, vy, vz), las derivadas parciales de estas velocidades respecto a cada dirección y respecto al tiempo, y sus derivadas de segundo orden, P es la presión del fluido y g la fuerza de la gravedad. El problema es que desconocemos una solución general para ese tipo de sistemas de ecuaciones, que los matemáticos llamamos no lineal de segundo orden.
La turbulencia
En los años treinta del siglo pasado, el matemático francés Jean Leray avanzó en el intento de resolución demostrando que existen soluciones (otra cosa es encontrarlas) y son únicas, pero solo localmente (en el entorno de un punto), definiendo conceptos que se aproximen a la solución (soluciones débiles) y probando su existencia, entre otras cosas. Muchos especialistas han venido trabajando en el tema desde su propuesta. Pero el asunto es aún más complejo por culpa de una característica adicional que presentan los fluidos: la turbulencia. No existe a día de hoy una explicación matemática rigurosa de cómo un fluido pasa de tener un flujo regular a uno turbulento. Ya Leonardo da Vinci observó en su tiempo la aparición de remolinos a diferentes escalas. Y los matemáticos han definido un concepto que cuantifica la rotación de un fluido dándole un nombre identificativo: el rotacional.
Leray conjeturó que el fenómeno de la turbulencia podría tener que ver con la existencia de lo que los matemáticos denominamos singularidades de las soluciones del sistema de ecuaciones. Para hacernos una idea de la complejidad del problema, el físico alemán Werner Heisenberg nos dejó una reflexión que ha quedado como un icono: “Cuando me encuentre con Dios, le haré dos preguntas: ¿Por qué la relatividad? y ¿por qué la turbulencia? Estoy seguro de que me sabrá contestar a la primera”.
En matemáticas, y en la ciencia en general, cuando nos encontramos estancados ante un problema, los investigadores tratan de hacerlo frente por otros caminos diferentes. Es como cuando un aventurero al escalar una montaña, o tratar de profundizar a través de la espesura de la jungla se encuentra con algo imposible de superar. Entonces busca otra vía que le permita llegar a donde desea. Y muchas veces esos nuevos enfoques nos permiten realizar nuevos descubrimientos. Este es el caso.
El meteorólogo Edward Lorenz se planteó en los años sesenta del siglo pasado la siguiente cuestión: resueltas las ecuaciones de Navier-Stokes, ¿podríamos predecir el tiempo meteorológico con mayor precisión y a más largo plazo? ¿Cómo es posible que conociendo exactamente las ecuaciones que rigen la circulación atmosférica y las condiciones de partida no se llegue a predecir con un grado de fiabilidad aceptable el tiempo que hará tres días después? Lo que hizo para experimentar fue simplificar extraordinariamente las ecuaciones, dando valores numéricos concretos y tratando de aproximarlas (en vez de en modo exacto, con números decimales). Tampoco consiguió resolver el “aparentemente sencillo” sistema. Pero encontró algo que nunca hubiera podido imaginar.
Al tratar las ecuaciones numéricamente, con los ordenadores de aquellos años, descubrió algunos comportamientos singulares:
1.- La evolución de cada una de las componentes de la solución era tan extraña que indicaba un comportamiento que parecía fruto del azar.
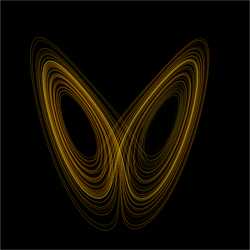
2.- Al representar gráficamente la sucesión de valores que toman las soluciones en el transcurso del tiempo, obtuvo una trayectoria que se enrolla sobre un curioso objeto de dos lóbulos. Dicho objeto, que atrae toda trayectoria, no tiene volumen, pero tampoco es una simple superficie. No era plano (aparentaba tener algo más que largo y ancho, dos dimensiones), pero no llegaba a ser tridimensional (largo, alto y ancho). Así apareció el primer “atractor extraño” (ver imagen; hoy se conoce como atractor de Lorenz) y motivó el estudio de la geometría fractal.
3.- Al querer rehacer con más detalle el cálculo de la solución para un tiempo largo, Lorenz introdujo en el ordenador los valores que había obtenido para un tiempo menor, observando que las soluciones no tenían ninguna relación con las previas. Se percató de que las soluciones dependían del número de cifras significativas consideradas en los cálculos (el ordenador proporcionaba seis decimales, pero la impresora sólo le daba tres). Este pequeño error crecía exageradamente lo que ponía en evidencia la sensibilidad del sistema de Lorenz respecto de las condiciones iniciales. Pequeñas variaciones provocaban soluciones muy diferentes (sistema mal acondicionado lo llamamos). Traducido a su campo de investigación, un mínimo error de observación cambiaba completamente el tiempo que haría al cabo de una semana. Lorenz bautizó este efecto con una imagen muy impactante y mediática, el Efecto Mariposa (El aleteo de una mariposa en Japón puede provocar un huracán en Los Ángeles), origen de la teoría del Caos. Esto zanjaba negativamente la posibilidad de conocer la evolución del tiempo que va a hacer en un plazo de tiempo largo, porque nos encontramos con un sistema impredecible. Cosas que prueban las matemáticas.

Para finalizar, un hecho que nos confirma una vez más que los descubrimientos realizados teóricamente, pueden tener aplicaciones insospechadas en el futuro. En el cine, cuando se deseaba quemar una casa, o que hubiera una inundación, literalmente se incendiaba un edificio real o una maqueta en el primer caso, y se utilizaba una gran piscina en el segundo. Hasta que, a Nick Foster, ingeniero de software, se le ocurrió hacer lo que a Edward Lorenz con las ecuaciones de Navier-Stokes: trocearlas quedándose sólo con aquellas partes que tratadas numéricamente en el ordenador fueran capaces de captar la esencia del movimiento del fluido que se desee representar (agua en su caso).
El ojo humano percibe una cantidad limitada de información, así que se le puede “engañar” sin que se dé cuenta. Dejó en las ecuaciones aquellas expresiones que transmiten la turbulencia y el chapoteo del agua de forma realista, despreciando el resto, hasta crear una imagen convincente. Y ganó el Oscar a los mejores efectos especiales por HormigaZ (1999) gracias a ello. Pero no sólo eso. Desde entonces, a partir del software que desarrolló con este procedimiento y otros que lo han perfeccionado, ya no hace falta que un especialista se queme bajo un chaleco ignífugo, ni haya que retocar los fotogramas o echar mano de maquetas para poder inundar completamente ciudades como Nueva York como se ve en la imagen de El día de mañana (2004). Permitan que me reitere: gracias a las matemáticas. Y eso que aún no hemos encontrado la solución general de las ecuaciones de Navier-Stokes, uno de los problemas que la fundación Clay premia con un millón de dólares al que lo resuelva. Aunque sinceramente creo que deberían incrementar ligeramente la recompensa, al menos proporcionalmente al número de años que lleve sin resolverse y a su utilidad, ¿no creen?
abc

